Fluid Mechanics and Aerodynamics

Direct and large eddy simulations of engineering and geophysical turbulent flows

We investigate, develop, and use numerical techniques of Computational Fluid Dynamics to study turbulence in gases and fluids. Highly accurate spectral and spectral element numerical methods are employed. We have introduced the Subgrid Scale Estimation Model for Large Eddy Simulations that allows physically realistic simulations of turbulence at greatly reduced numerical resolution and computer cost. We are using Direct and Large Eddy Simulation techniques to investigate properties of a variety of important turbulent flows: boundary layers, wakes, convection, rotating and stratified flows. Our interests are in both fundamental and applied aspects of turbulence.

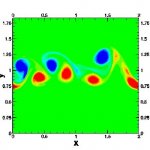
Example: vortices developing in a wake of a bluff body moving in a stratified fluid.

The study of geophysical fluid flows has taken on a new popularity, and urgency, with an increasing awareness of the complexity and delicate balance of the intermediate and large scale motions of the fluids in which all life on earth occurs.

The physical problems typically involve an interaction between the usual equations of motion for a homogeneous fluid, together with additional constraints arising from the planetary rotation, or density stratification. Motion at interfaces between fluids of different densities can give rise to linear and nonlinear waves, and the interaction between waves and turbulence is also a recurrent theme. As is usual in much fluid mechanics research, progress depends on the close interaction and collaboration between theory and experiment (laboratory or numerical), and the work at USC exmplifies this approach. We also maintain close collaborations with several international facilities, including the research groups at the Coriolis Facility in Grenoble, and the LadHyX group at Ecole Polytechnique, Paris.

Past Projects

Turbulence in stratified fluids

Turbulent wakes in stratified fluids

Faculty: Spedding, Fincham
The initially turbulent flow behind a bluff body moving through a stratified fluid forms a wake in which motions are confined largely to the horizontal, vertical velocities being very small. In this sense the late wake flow can be termed quasi-2D. The velocity field can be separated into vortex and wave components by taking the curl and the divergence, respectively. The wakes that evolve in the presence of stratification have a much higher degree of coherence in the vorticity field than their 2D, homogeneous counterparts, and quantitative measurements show order of magnitude differences.

Quasi-2D turbulence in stratified flows

Faculty: Fincham, Spedding
Investigations of laboratory grid turbulence show how it differs substantially from both full 3D turbulence, and also from the pure 2D case that has been studied primarily in DNS. In many respects, however, it is a good model of ocean and atmospheric motions at large and meso-scales, and so current work aims at formulating a quantitative model for the physical mechanisms of most importance in the dissipation and transfer of kinetic energy amongst different scales.

N-layer vortex dynamics

Faculty: Newton
Multi-layer fluid models are being analysed where the vorticity dynamically evolves within each layer. Of interest is the alignment of vorticity and the ability of vorticity to transport particles across layers. Chaotic and integrable aspects of the models are being analysed from the Hamiltonian point of view.

Atmospheric Flows:

N-vortex problems on a sphere

Faculty: Newton
The dynamics of vorticity on a rotating sphere are being considered by Newton and students. Point vortex approximations and numerical simulations are used to track the evolution of vorticity and the transport of particles on the surface of a sphere. Weather patterns are being analysed and compared with the topological streamline patterns generated from the models, both from the kinematic and dynamic points of view. A project is underway to topologically `decompose’ sequences of weather patterns and to characterize their complexity.

Convective flows:

Coupled internal waves and convective instabilities

Faculty: Redekopp
Convective instabilities can play an important role in geophysical fluid mechanical systems, with applications in convective mixing events in both the atmosphere and in bodies of water. This project investigates the coupling between internal waves and convective instabilities which occur in interactions of the ocean thermoclinic layer and the upper mixed layer. The problem is being approached from both an analytical and an experimental basis.

What is Turbulence?

Fluid turbulence was identified in 1949 by Von Neumann, one of the founders of modern computers, as one of the remaining grand challenges in physics. Today, almost 50 years later, it still is. It is a problem in applied physics, because almost certainly the equations for the physical mechanisms can be written down by anyone who has ever taken an undergraduate fluid mechanics course. The Navier-Stokes (NS) equations apparently contain all of turbulence, and so in a limited sense, there is no problem to be solved.

Knowing the existence of a set of equations is of course not all the same thing as being able to solve them, or to know when solutions exist either mathematically, or in the physical world. The presence of nonlinear terms in the NS equations renders their direct solution impossible for all but the most carefully-chosen of problems. The degree of nonlinearity is determined by the Reynolds number,

Re = (ρ U L)/μ .

U and L are velocity and length scales, respectively, and ρ and μ are the fluid density and viscosity. Re thus represents the ratio of inertial to viscous forces. When Re is very low, around 1, viscous forces are dominant, and the nonlinear terms in the NS equations are very small. Solutions of the NS equations exhibit many symmetries, that are broken as Re increases. With Re sufficiently high, solutions to the NS equations can be very complex, but in a statistical sense, certain symmetries are recovered. This state of ‘fully-developed’ turbulence has been studied for many years, and a large number of explicit and ingenious statistical theories and predictions have been made for the behavior of fluid flows in this regime. The fluid state known as fully-developed turbulence has certain characteristic properties, which both describe the flow and give hints as to its engineering importance.

Turbulence Books

There are many of these, of course, but here is a list of finite length that includes some classics and favorites.

• Tennekes H & Lumley JL 1972 A First Course in Turbulence MIT Press.
• Hinze JO 1959 Turbulence McGraw-Hill
• Batchelor GK 1953 The Theory of Homogeneous Turbulence Cambridge
• Hunt JCR, Philipps OM & Williams D 1991 Turbulence and Stochastic Processes: Kolmogorov’s Ideas 50 Years On Royal Society of London
• Sirovich L 1991 New Perspectives in Turbulence Springer-Verlag
• Lesieur M 1993 Turbulence in Fluids Kluwer
• Frisch U 1995 Turbulence Cambridge
• Wilcox D 2006 Turbulence Modeling for CFD, 3rd ed., DCW Industries

Fluid turbulence is:

irregular — turbulent motions are impossible to predict in detail, except in a statistical sense. The terms chaos and turbulence are frequently used interchangeably, but it is not so clear that chaotic motions are necessarily or usefully involved in turbulence at high Reynolds numbers. Chaos is a dynamical systems description that obtains when very complex motions in n-dimensional phase space can be produced even when n is not very large. In fluid turbulence n, the number of degrees of freedom, is typically very large. A description in terms of chaotic attractors will not neceesarily be either feasible or useful.

dissipative — viscous shear stresses increase the internal energy at the expense of kinetic energy. Often when we wish to maintain the kinetic energy of a fluid flow, turbulence is a significant impediment.

everywhere — one could argue that laminar, non-turbulent flows are artifacts of carefully-constructed wind tunnels and/or special theoretical models by humans with finite cranial capacity. At most commonly observable scales, fluid flows are turbulent. This includes the atmosphere that surrounds us, and the ocean flows that cover most of the earth’s outer surface, and in all likelihood the core flows themselves.

diffusive — turbulence encourages mixing, and diffusion of chemical species or tracers (including temperature) is accelerated by the complex inter-scale interactions that occur in turbulence.

active over a large range of scales — as indeed implied by the large values of Re, turbulence occurs over a broad range of scales. Over this range of scales, turbulence is dynamically similar. A cascade of self-similar inter-scale interactions eventually culminates in viscous dissipation at the very small scales, which are still much larger than molecular.
We must go to extremes in order to fabricate flows that are non-turbulent. Research wind-tunnels and water channels, for example have very careful design of shape and flow conditioning honeycombs and screens, simply to keep the velocity fluctuations down to manageable proportions.